I implemented Suffix Tree algorithm in Python in the past few days, you can refer to my github repository if you’re interested in. The famous tutorial on stackoverflow is a good start. If you pay enough attention to some details like state updating or suffix links managing, you can write the code by yourself for sure. When a lot of small operations are entangling together, the ancient trick flowchart is always a wise choice for assisting. Also a tree visualizer might help a lot with debugging for sure. In order to make the intervene of the processes easy to understand, we demonstrate the flowchart in this post.

Main Process

I composed a program without the help of a flowchart at the beginning, and it could handle a lot of strings well enough. However, when I tried a long and weird string, it failed. I gave up the original codes after 3 days of attempts. I picked up a piece of paper, and drew the flowchart bit by bit. Literally, for the first time, I felt the power of a flowchart.

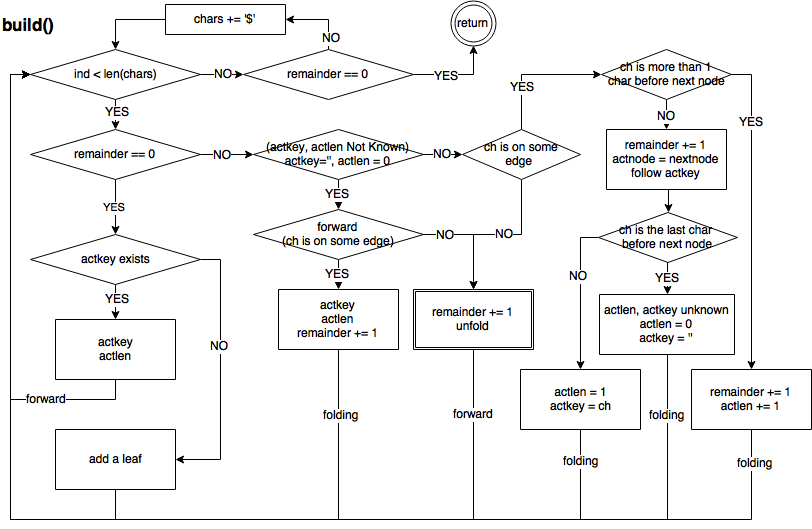
You can start checking out diagram from the top-left, will experience judging block, moving operation, variables updating and so on. The special cases, for example, where split is required, moving forward is required, interrupting the current unfolding process is required and so on, are treated respectively. Complex operations such as moving, unfolding, split, and suffix links maitainance are extracted as separate functions as below.

Operations

Move

• There’re two different types of moving operation.
  • hopping- which is used when we have to hop node-by-node untill we reach the actual node to do the next operation.
  • stepping- Stepping is used when the active node is right, but the next operation should be imposed in the middle of the edge, we need to move char-by-char on the edge to the right position.

Fig.2 Moving Operations	Fig. 3 Unfolding Operation

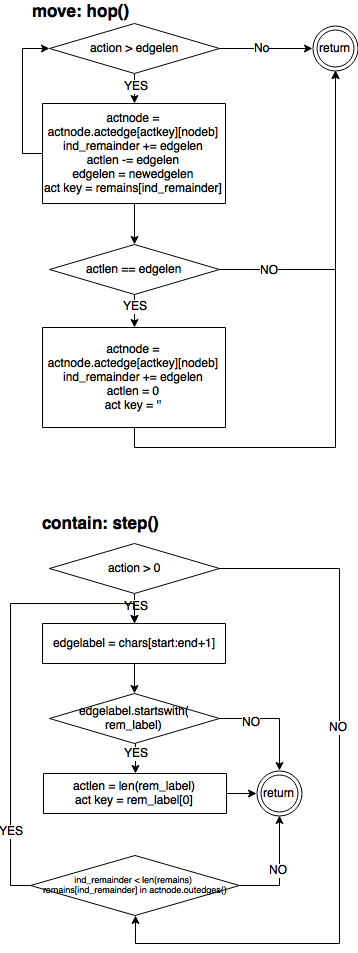• Forward stepping, folding and unfolding operations need move forward along the original string to find the unfolding point, but they are different:
  • During advancing and folding, we compare edge labels with the ORIGINAL string to find out the first different chars to finish the folding operation, produce a REMAINS string to be unfolded, and a actnode, actkey, actlength, remains, and ind_remain (which is the current act_index in REMAINS string while moving)
  • During unfolding, we compare edge labels with REMAINED string to find out the first different chars to start the edge splitting operation, consume the REMAINS string till it is exhausted (or unable to proceed). ind_remain is like the landmarks for current proceeding to the actual unfolding point (which is necessary when node jumping is needed).

UNFOLDING

Unfolding operation is triggered when we find the first different chars, specifically during the folding process as we are comparing the current char in the original string and the current char on the current active edge.

Observation 1

Depending on the LENGTH of a suffix link chain, to exhaust the REMAINS string needs either one single continuous unfolding process, or multiple unfolding process (processes other than the very first should be restarted from root node).

Observation 2

When the string is not well-ended (forward move fails to find a different char to split), we need to append a unique char (e.g., '$') to the end of the string.

Observation 3

Termination of current unfolding process includes 2 situations:

• REMAINS string is exhausted,

1
2
3
4
5
6
7
8
9
    If (suffix links have been exhausted, but REMAINS string is not exhausted yet):
        Go to the root node,
        get actkey by shortening the REMAINS by 1 char from head,
        restart the process,
    repeat till REMAINS string is exhausted.

    If (REMAINS string is exhausted before suffix links are exhausted):
        Terminate.
    

• REMAINS string is not exhausted,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
    If (REMAINS string is totally inside a path, and
     no different character can be found on this path,
     ORIGINAL string has not been exhausted in the outside forward moving process):
        Keep the REMAINS,
        Move forward to find another different char from the ORIGINAL string,
            moving start from current actnode, along current actkey,
            change actlength, REMAINS, and ind_remain accordingly.
        If the REMAINS stop decreasing,
            terminate the current unfolding
            (means stop adding suffix link for another edge split for this step).

    If (REMAINS string is totally inside a path, and
      ORIGINAL string has been exhausted by this REMAINS):

        If (this string is unable to be finished):
            append a reserved char like '$' to terminate it.
        If (REMAINS string stop increasing):
            terminate this step,
            stop adding suffix links for current step.
    

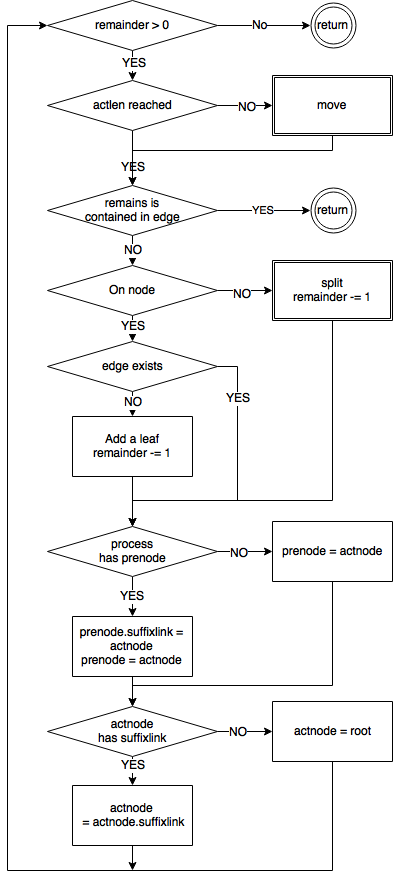
SPLIT

Depending on the position of the actkey, a SPLIT can happen on a node or an edge.

• on node, then add a new branch, update actnode, actlength, actkey, REMAINS, ind_remain accordingly.
• on edge, then split the edge, add a new node, and add a new branch, change the variables accordingly.

SUFFIX LINK

Before the end (stopping shortening REMAINS string) of a unfolding process, add lately split (or should be split but has already been split before) node to the previously split node. There are some important rules and observations from stackoverflow, we need to stick strictly to the them in order to make the moves right.

Rule 1

If after an insertion from the actnode == root, the actlength > 0, then: actnode = root, actlength -= 1, ind_remain += 1, actkey = REMAINS[ind_remain]

Rule 2

If we split an edge or add a leaf on an internal node, and the current actnode is not the first expanded node in this round of unfolding process, link the previous actnode to this actnode with a suffix link.

Rule 3

After an expand (either split and edge or only add a leaf) at actnode != root, then: follow the suffix link set the actnode = suffixlink, if suffixlink is None, set the actnode = root, either way, actlength, actedge stay unchanged.

Observation 1

When the char we want to add to the tree is already on the edge, we update actkey, actlength, and remainder respectively.

Observation 2

When the final char we need to insert is found to exist in the tree already, we update the remainder, actkey and actnode accordingly, although the tree is not changed, but the operation here should be taken as an expansion, which means suffix link should be added to its previously expanded one.

Code in Python

Code Link

Python: Ukkonen’s Suffix Tree Algrithm

Some Challengable Examples

1
2
3
4
docs = ['abcabxabcd', 'dedododeeodoeodooedeeododooodoede$', 'ooooooooo', 'mississippi']
for text in docs:
    tree, pst = build(text, regularize=True)
    Node.draw(tree, pst, ed='#')

References

• Tutorial on Stackoverflow